这些排序都是比较经典的排序算法:
- 冒泡排序
- 选择排序
- 插入排序
- 归并排序
- 快速排序
- 计数排序
- 桶排序
- 基数排序
那么如何使用python来实现这些排序呢?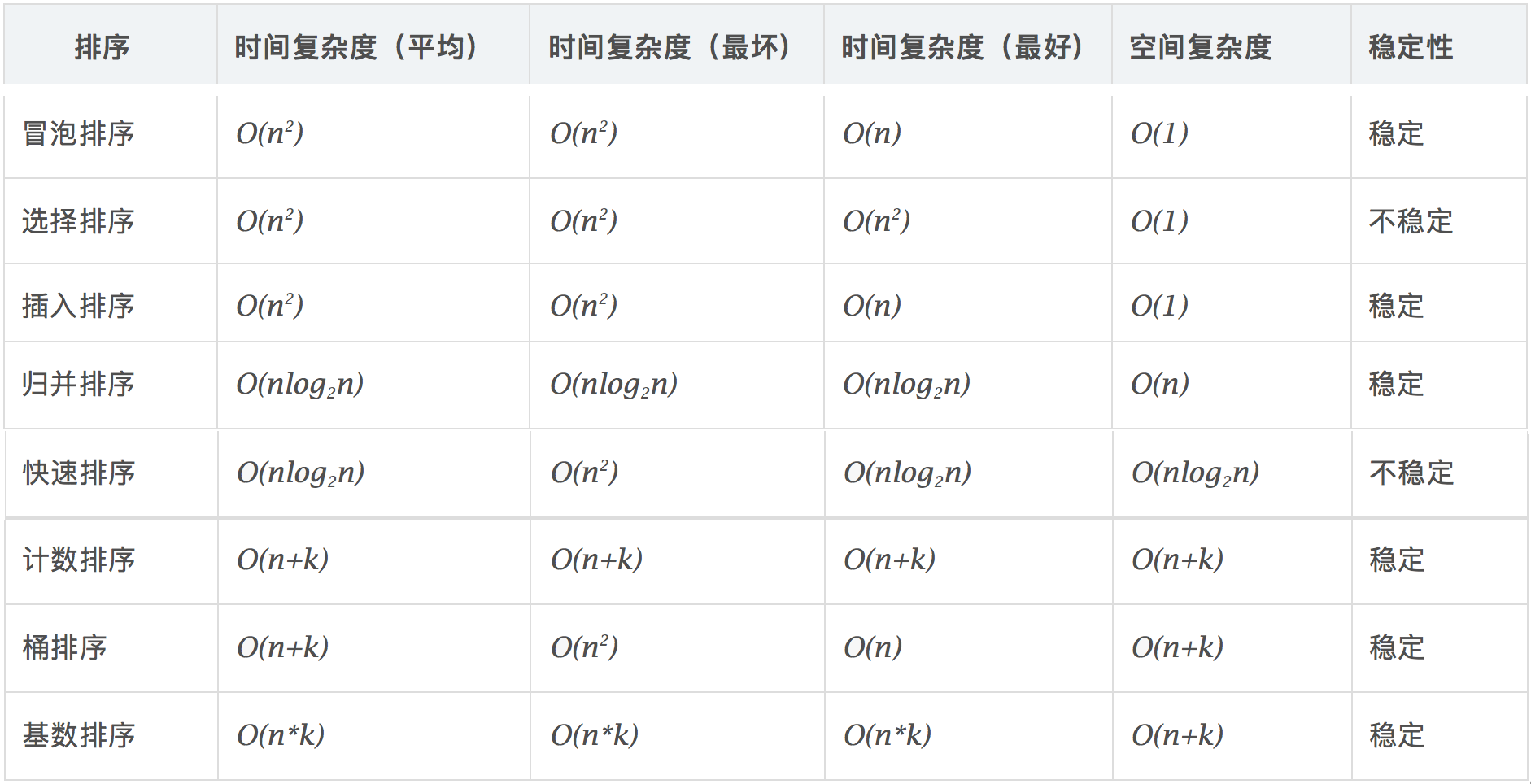
冒泡排序
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个。
重复以上步骤,直到排序完成。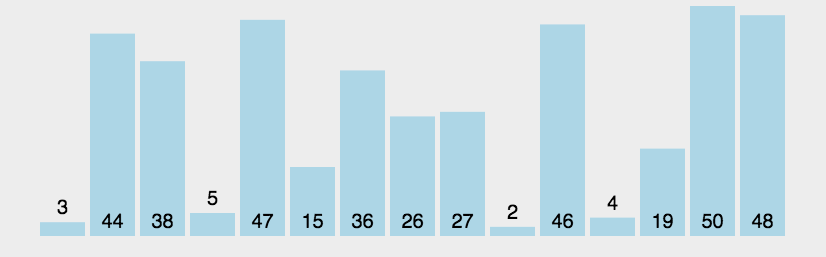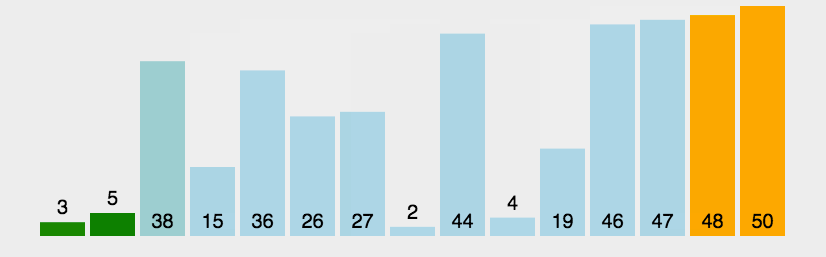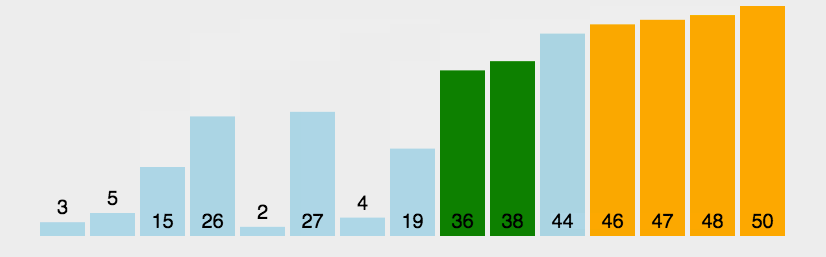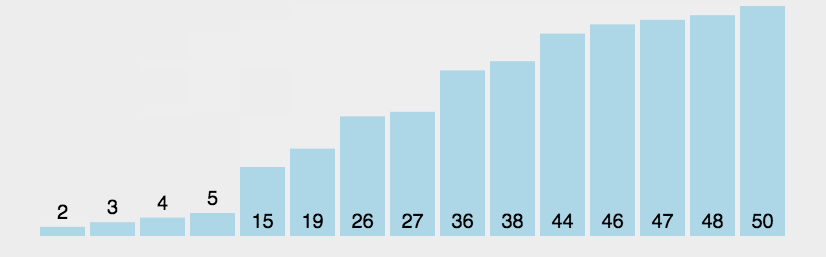
1 | def Bubble_Sort(): |
选择排序
- 在未排序序列中找到最小元素,存放到排序序列的起始位置;
- 再从剩余未排序元素中继续寻找最小元素,然后放到已排序序列的末尾。
重复以上步骤,直到排序完成。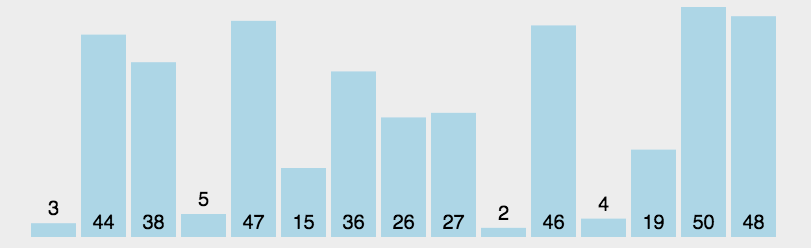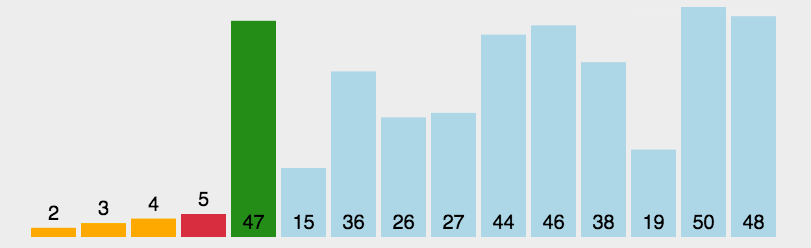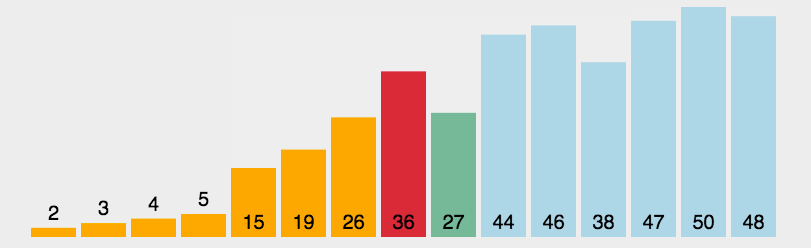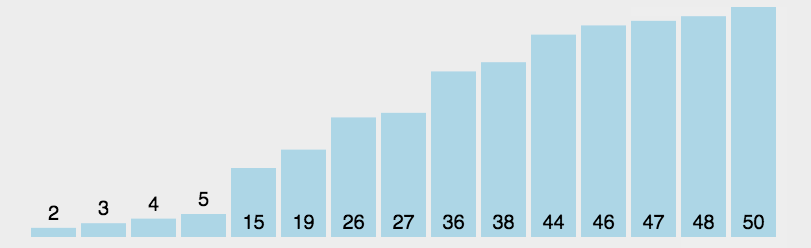
1 | def Select_Sort(): |
插入排序
- 从第一个元素开始,该元素认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后。
重复步骤2~5,直到排序完成。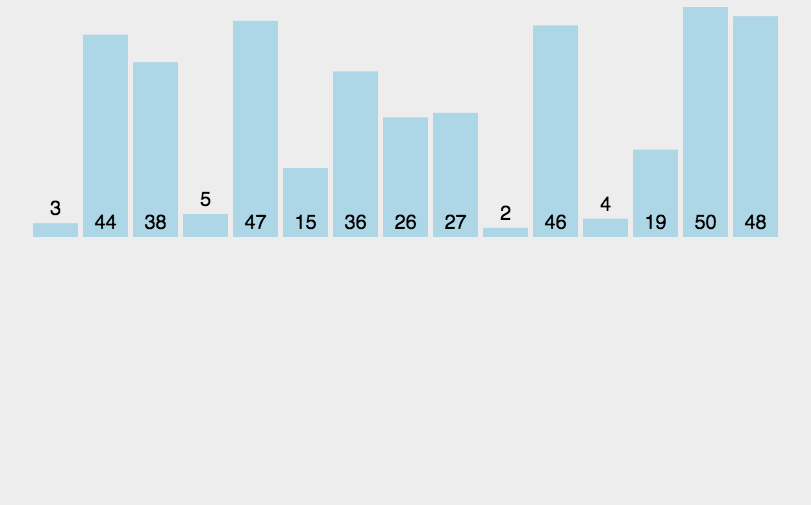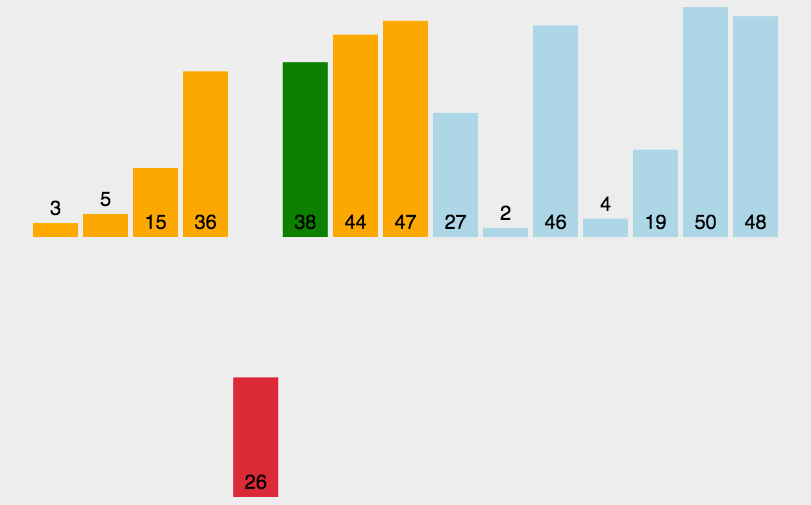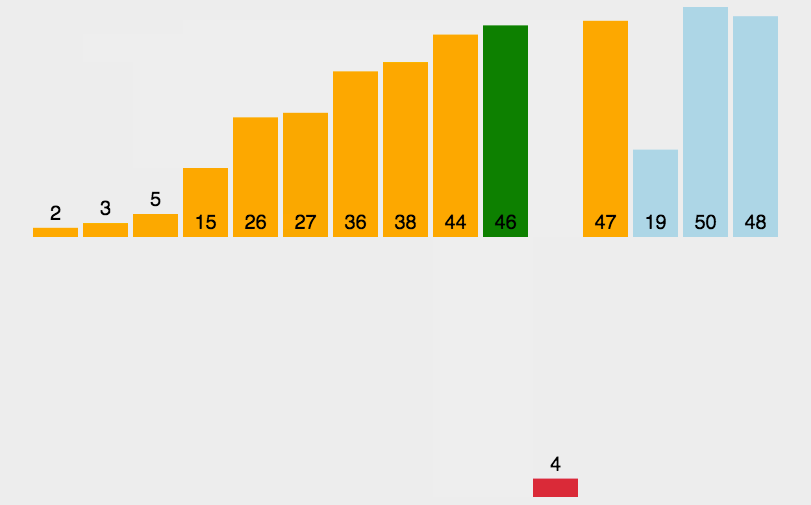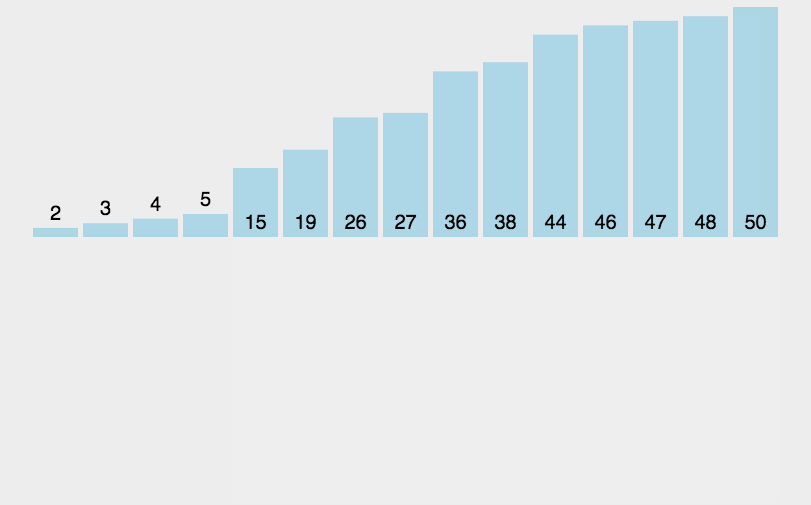
1 | def Insert_Sort(array): |
归并排序
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
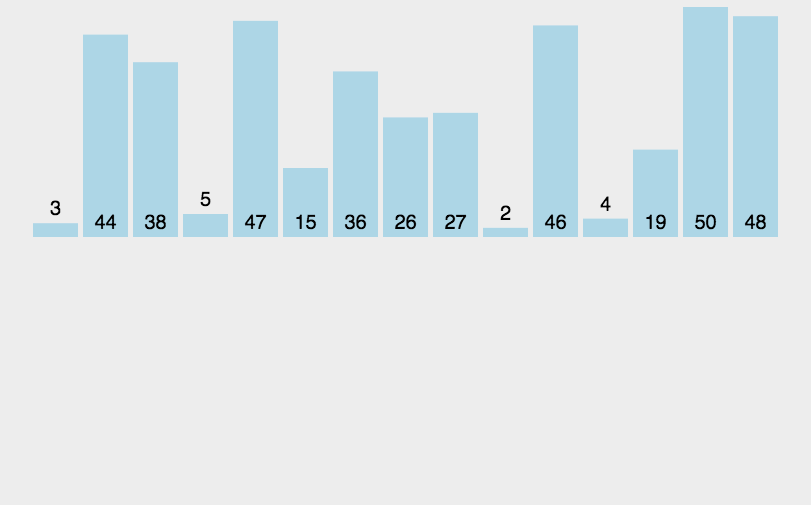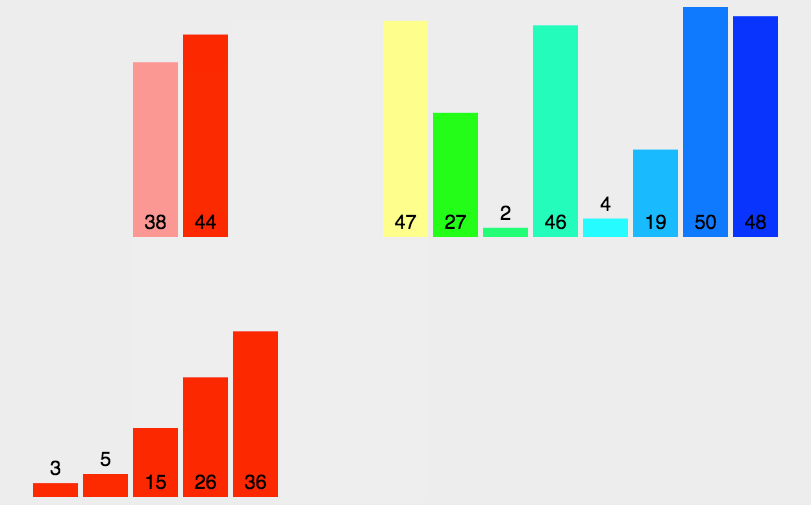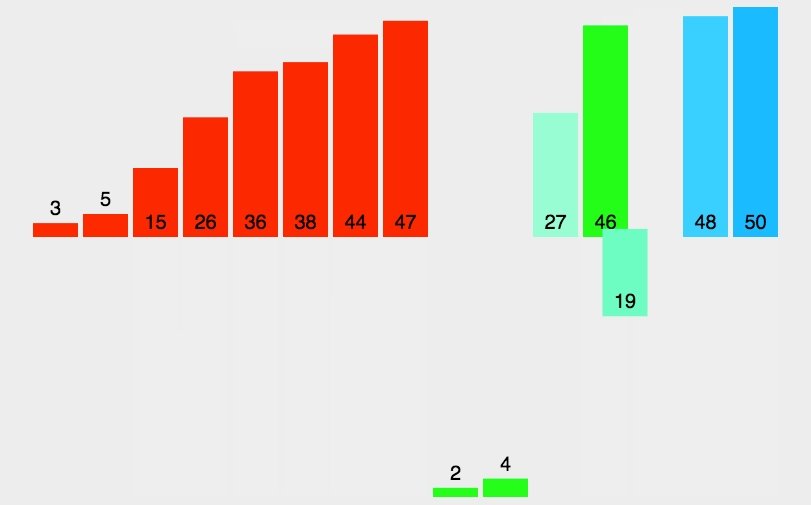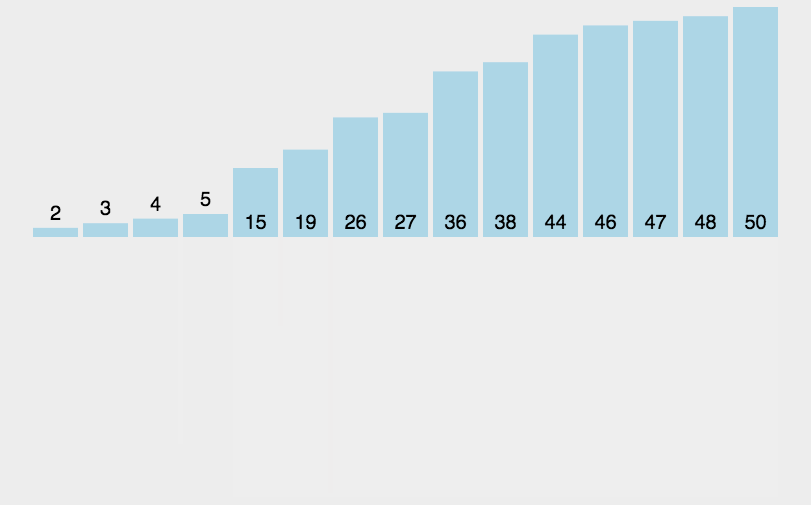
1 | def Merge(array_1, array_2): |
快速排序
- 从数列中挑出一个元素,作为一个基准(pivot);
- 重新排序数列,将所有比基准值小的摆放在基准前面,所有比基准值大的摆在基准的后面(相等的可以分到任一边),于是该基准就处于数列的中间位置。
- 递归地把小于基准值元素的子数列和大于基准值元素的子数列排序。
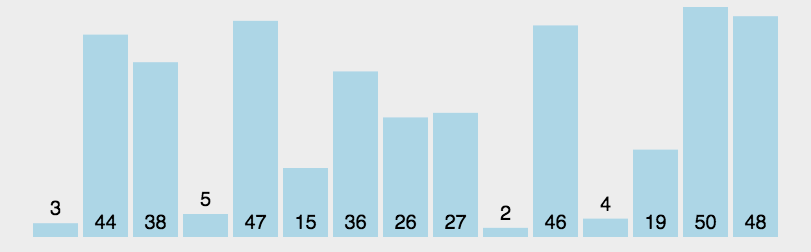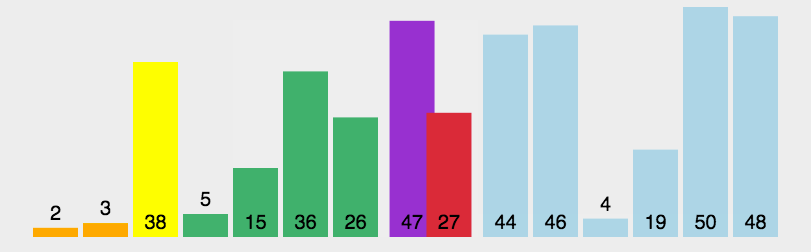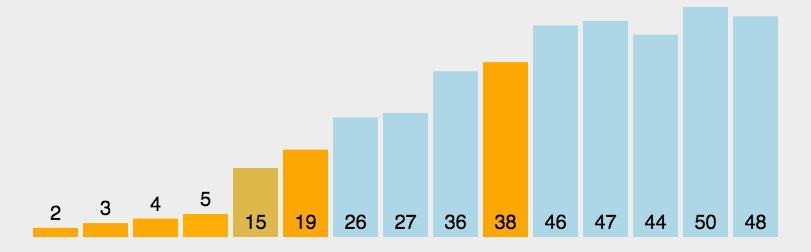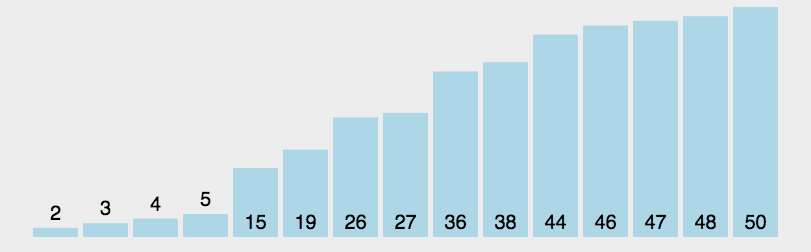
1 | def Quick_Sort(array, left, right): |
计数排序
- 找出待排序的数组中最大和最小的元素;
- 统计数组中值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项值和前一项相加);
- 反向填充目标数组——将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
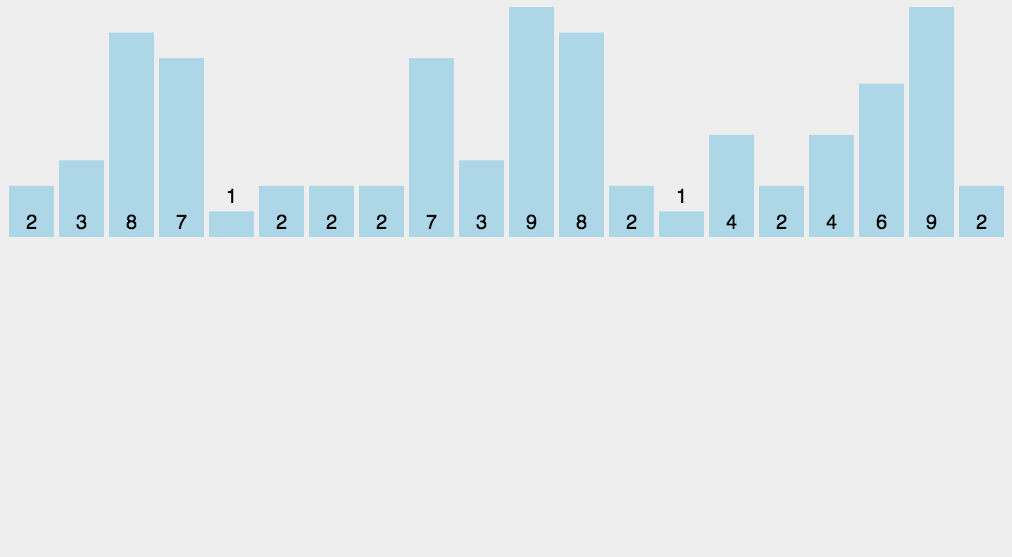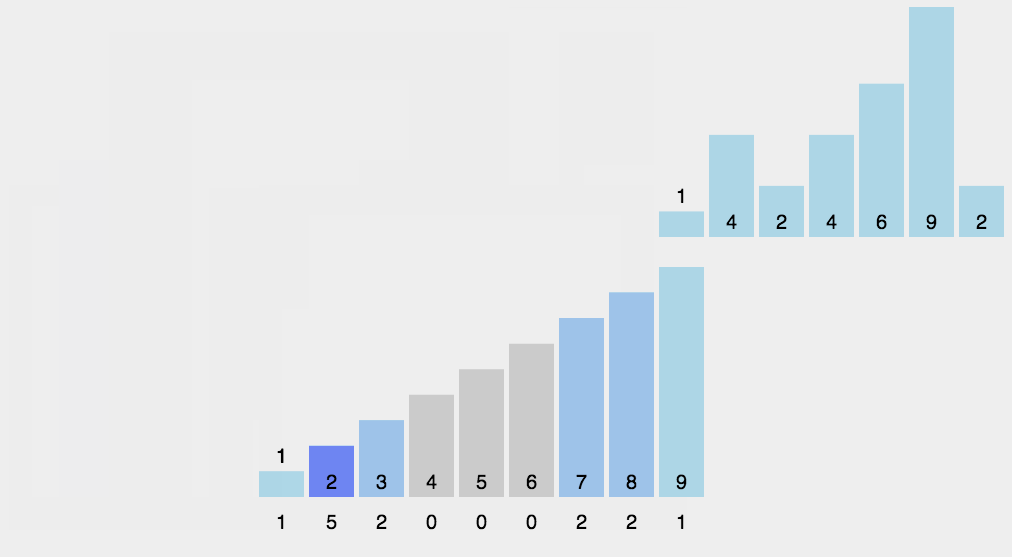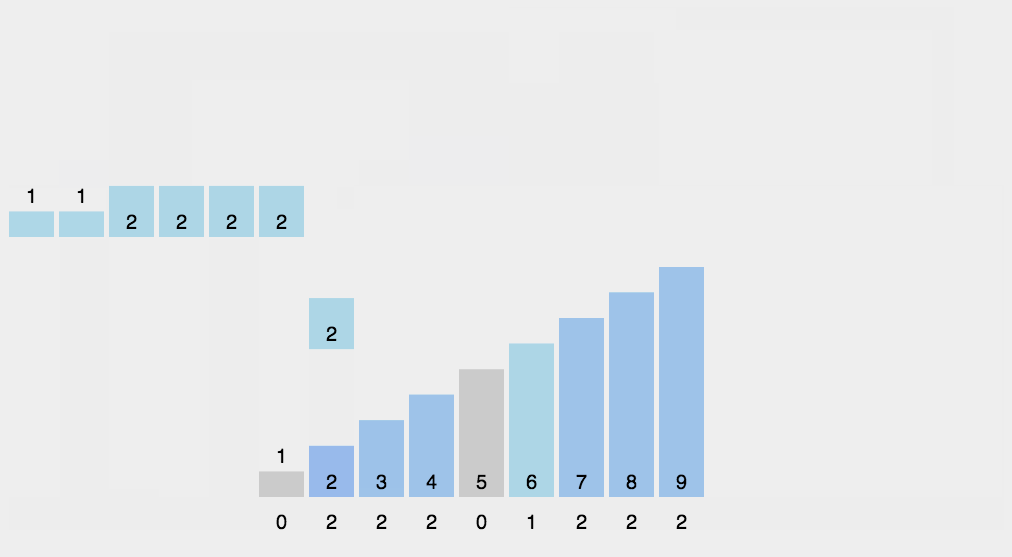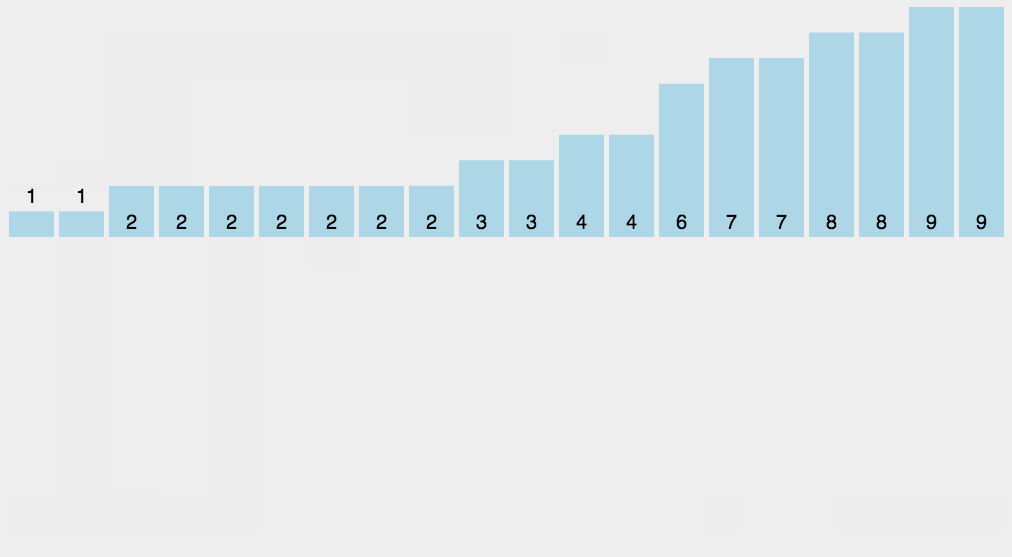
1 | def Count_Sort(): |
桶排序
- 设置一个大小定量的数组A当作空桶;
- 遍历一组数据,并且把数据一个一个放到对应的桶里去(数i放入A(i));
- 遍历桶数组,对每个不是空的桶进行排序;
- 从不是空的桶里把排好序的数据拼接起来。
1 | def Bucket_Sort(): |
基数排序
- 取得数组中的最大数,并取得其位数;
- 假设arr为原始数组,从最低位开始取每个位组成radix数组;
- 对radix进行计数排序。

1 | def Radix_Sort(array): |

