Fork me on GitHub

C++实现各种查找算法

发表于 | 分类于
字数统计: 726 字 | 阅读时长 ≈ 3 分钟

顺序查找

顺序查找也称为线形查找，属于无序查找算法。从数据结构线形表的一端开始，顺序扫描，依次将扫描到的数与给定值k相比较，若相等则表示查找成功；若扫描结束仍没有找到关键字等于k的结点，表示查找失败。

1
2
3
4
5
6
7
int SequenceSearch(int a[],int value,int n){
    int i;
    for(i=0; i<n; i++)
        if(a[i]==value)
            return i;
    return -1;
}

二分查找

二分查找也称为折半查找，属于有序查找算法(给定数列必须有序)。用给定值k先与中间结点的值进行比较，分成两边进行递归查找，直到查找到k或查找结束。

1
2
3
4
5
6
7
8
9
10
11
int BinarySearch(int a[],int left,int right,int k){
	int mid=(left+right)/2;
	if(a[mid]==k)
		return mid;
	else{
		if(k<a[mid])
			erfen(left,mid,k);
		else
			erfen(mid+1,right,k);
	}
}

插值查找

插值查找也属于有序查找，可以说是二分查找的一种特殊版本，二分查找中查找点计算如下：
在二分查找中，mid=left+1/2*(right-left);
而插值查找中：mid=left+(k-a[left])/(a[right]-a[left])*(right-left);
实际上就是优化了mid，根据关键字在整个有序表中所处的位置，使得mid更加接近k的位置，从而减少了比较次数，提高查找效率。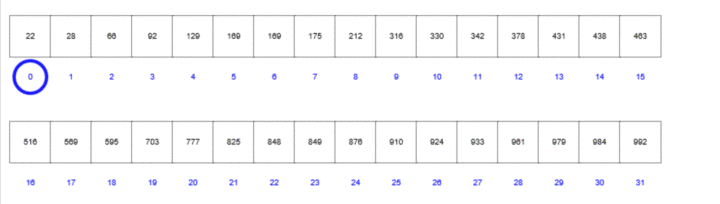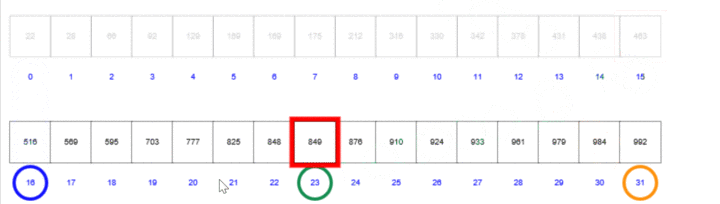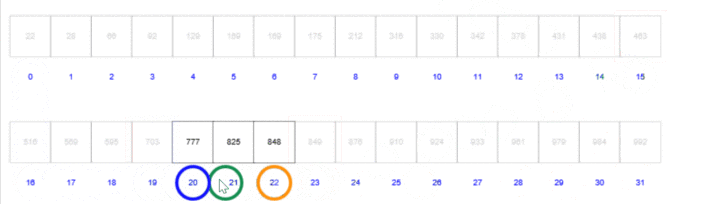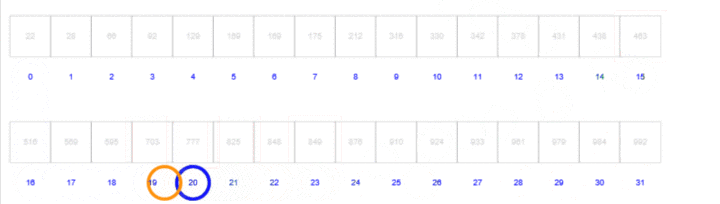

1
2
3
4
5
6
7
8
9
int InsertSearch(int a[],int k,int low,int high){
    int mid = low+(k-a[low])/(a[high]-a[low])*(high-low);
    if(a[mid]==k)
        return mid;
    if(a[mid]>k)
        return InsertionSearch(a, k, low, mid-1);
    if(a[mid]<k)
        return InsertionSearch(a, k, mid+1, high);
}

分块查找


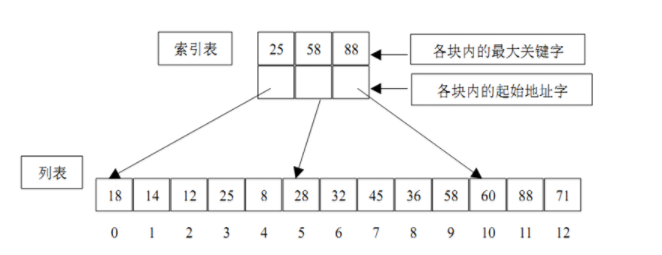
分块查找又称为索引顺序查找，它是顺序查找的一种改进方法。也就是将一组数据元素“按块有序”划分为m块(每一块中的数据元素不必有序，但块与块之间必须“按块有序”)。
然后确定k所在的块，在那一块使用顺序查找进行查找。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
struct index{
    int key;
    int start;
    int end;
}index_table[4];

int block_search(int a[],int k){
    int i,j;
    i=1;
    while(i<=3&&k>index_table[i].key)
        i++;
    if(i>3)
        return 0;
    j=index_table[i].start;
    while(j<=index_table[i].end&&a[j]!=k)
        j++;
    if(j>index_table[i].end)
        j = 0;
    return j;
}

调用示例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
int main(){
    int j=0,k,pos,a[16];
    for(int i=1;i<16;i++)
        scanf("%d",&a[i]);//输入15个数(从小到大)
    for(int i=1;i<=3;i++){
        index_table[i].start=j+1;//每个块范围的起始值
        j=j+1;
        index_table[i].end=j+4;//每个块范围的结束值
        j=j+4;
        index_table[i].key=a[j];//每个块范围中的最大值
    }
    printf("input k:");
    scanf("%d",&k);    //输入要查询的数值
    pos=block_search(k,a);    //调用函数进行杳找
    if(pos!=0)
        printf("%d",k);
    else
        printf("-1");
    return 0；
}

除此之外，还有二叉树查找，哈希查找，斐波那契查找等。